《博士熱愛的算式》(日語:博士の愛した数式)一本關於數學的小說
三版九刷 2014年1月 ISBN:978-986-173-681-5
作家:小川洋子 (本名:本鄉洋子) 早稻田大學第一文學院文藝系畢業
2004年時獲得第一屆書本大獎及第五十五屆讀賣文學獎,《博士熱愛的算式》為小川洋子代表作。
譯者:王蘊潔
小說其後被改編成電影《博士熱愛的算式》,於2006年1月21日公映。
電影導演:小泉堯史。演員:由寺尾聰、深津繪里主演。
我和兒子都叫他博士。博士則叫我兒子「根號」,因為兒子頭頂平坦得像根號。
「哇,裡面應該裝了一個聰明的腦袋。」
博士摸著兒子的頭說道,絲毫沒有把兒子的頭髮弄亂了。兒子充滿警戒地縮著脖子,他不喜歡同學拿這件事和他開玩笑,所以平時整天帶著戴著帽子。
「只要使用根號,就能給無窮的數字、肉眼看不到的數字一個明確的身分。」(p3)
故事是這樣開頭的。一本感性的文學小說,以理性的數學符號當開端,樂趣就在這看似矛盾的衝突中,精彩之處就在二者的交錯輝映。
故事的主角有,
博士 因車禍而導致記憶出現障礙,記憶只有80分鐘。擁有數學博士學位。
我 提供敘事觀點的角色。女管家,獨力扶養兒子。
根號 女管家的兒子。因為頭頂平坦,而被博士起了這個暱稱。
寡婦 博士哥哥的妻子。由於55歲時,發生交通意外,所以現在腳不太好。
本書一本關於數學的小說,作者以「數學」為架構,鋪陳一段感人的故事。那麼就從「數系」討論起,但如果您對數系的定義不感興趣,那就先跳過這一段,有需要瞭解的時候再回頭來看。
【數學世界】
數字
阿拉伯數字的起源,是由古代印度的婆羅米人發明,後經由阿拉伯傳入西方。現代所稱的阿拉伯數字以十進制為基礎,採用0、1、2、3、4、5、6、7、8、9共10個計數符號。
自然數 0、1、2、3、4、5、6、7、8、9、10、11.....
最常用的數為自然數,有些人稱為正整數,有些人則稱為非負整數。在十進位數字系統裡,自然數的標記符號為0至9等十個數字,將以十為基數的進位制使用在大於九的數上。 因此,大於九的數會有兩個或兩以上的位數。表示所有自然數的集合為{N}。
「像女王般美麗高貴,也像惡魔般殘酷。其實說起來簡單,就是研究誰都知道的正整數1、2、3、4、5、6、7.....得關係」(p55)
整數 -1、0、1、2......
負數是小於0的數,通常在其前面加上一負號,來表示其為正數的對立。 負整數、正整數和零三者即合稱為整數{Z}。
有理數 1/3、5/4
0到1之間還有數字嗎?(連續二個整數間還有數字嗎?)數學上,有理數是指一可以被表示成整數分子(m)和非零整數分母(n)的分數的數(m/n)。分數可以是正的、負的、或零。整數及分數合稱為有理數{Q}。
以十進位標記的有理數,其位數會中斷或一直重覆。例如,分數 5/4 能夠寫做中斷位數的十進位數 1.25。分數 1/3 只能夠寫做 0.3333...(無限的3)。
無理數 根號2(記為![]() )、圓周率(
)、圓周率( )、自然對數的底(e)
)、自然對數的底(e)
一個等腰直角三角形,二邊長皆為1,斜邊長為根號2(記為![]() )。這是數學史中,最重要的平方根,是第一個公認的無理數,也叫畢達哥拉斯常數。
)。這是數學史中,最重要的平方根,是第一個公認的無理數,也叫畢達哥拉斯常數。![]() =1.4142135623.......,因為無法理的清楚,所以數學家稱他為無理數。
=1.4142135623.......,因為無法理的清楚,所以數學家稱他為無理數。
無理數是不能被寫成分數的數,若以十進位標記的無理數,其位數不會重覆且不會中斷。
實數
不嚴謹地說,實數可以被用來表示量度,而且對應至數線上的點,可以和一連續的直線數線視為同一事物,意即「實在的數」。實數包含有理數及無理數,實數的符號為{R}。
虛數
負1的平方根( ![]() )是多少?此數在實數中是找不到的,聰明的數學家想出了一套解決的方法,將思想移動到更多層次的抽象世界。歷史上,此數的誕生源自於如何將負1取平方根的問題。負1的平方根,此數被標記為
)是多少?此數在實數中是找不到的,聰明的數學家想出了一套解決的方法,將思想移動到更多層次的抽象世界。歷史上,此數的誕生源自於如何將負1取平方根的問題。負1的平方根,此數被標記為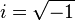 。
。
複數
包含實數與虛數。表示所有複數的集合為{C}。
小說如果這樣寫,鐵定賣不出去,不過這是閱讀筆記,隨我高興怎麼寫。為什麼要這麼麻煩的介紹數字的分類呢?因為故事的開端,「只要使用根號,就能給無窮的數字、肉眼看不到的數字一個明確的身分。」無窮的數字包含的就是實數、肉眼看不到的數字就是虛數。
虛數與靈魂
本書以數學為架構,描述博士、管家、根號、寡婦四個人的互動。數字原本存在於距離文字最遙遠的地方,但數字卻成為故事中,角色靈魂溝通的媒介,數字仍然有故事。
「現在,把-1放進去試看看。」
博士說道。
「只要把相同數字成二次,變成-1的話就行了吧?」
......
博士絕對不會催促我們,他喜歡看我和兒子陷入沈思的樣子。
「應該沒有這樣的數字吧。」我戰戰兢兢說道。
「不,在這裡。」
他指著自己的胸口。
「這是個很拘謹、謹慎的數字,不會現身,卻在我們的心裡,用一雙小手支撐這個世界。」(p5)
虛數是數線上無法表達的數,但博士卻指著自己的胸口,說「它」存在於我們的心裡。如果實數比喻為一個人的話,那麼虛數就是人的靈魂,用一隻小小的手(i)支撐這個世界。在我們生活的世界裡,除了有形的動物、植物之外,還有看不到的靈魂的存在,生命既是由生物與靈魂所共同構築而成的。從自然科學的角度來看,如果把實數比喻成物質的話,那麼虛數就是能量,少了能量,世界將會變得冰冷。(物質佔有空間具有質量,能量不佔空間不具質量)
數字的問候
「你穿幾號鞋子?」
聽到我自報是新來的管家,博士的第一個問題不是問我的名字,而是我鞋子的尺寸。既不問候,也不點頭打招呼。身為管家,無論任何狀況也不能用問題回答雇主的問題;基於管家手則這項規定,我如實回答了博士的問題。
「24號。」
「哇,多純潔的數字,是4的階乘。」
「你家的電話號碼幾號?」
「5761455。」
「5761455嗎?真了不起。這是1億以下的質數總數。」
我們會用什麼語言與別人溝通呢?遇到種菜的老阿伯,我們會說:「甲爸沒?」遇到年輕的小姐,我們會說:「你今天真漂亮!」遇到老外,我們會說:「How do you do!」遇到不同的人,我們會選擇不同的語言來表達問候,而博士則使用他最熟悉的語言:「數字」。
【數學世界】
階乘 4的階乘 4!=1×2×3×4=24......正好是管家鞋子的尺碼24號
質數 指在大於1的自然數中,除了1和此整數自身外,無法被其他自然數整除的數(2, 3, 5, 7, 11,......)
根據中央大學單維彰教授的 私人書評:
一億以下共有 576-1455 個質數嗎(女管家的電話號碼,p.10)? 誰會記得這種事?誰會想到用這個數來作文章? 出於好奇,我用 Maple 的 ithprime() 指令, 問第 5,761,455 個質數是什麼(2 是第一個質數)? 得到 99,999,989:九千九百九十九萬九千九百八十九。 下一個質數是 100,000,007:一億零七。真有趣, 超過一億的第一個質數是一億加七, 在那之前有五百七十六萬一千四百五十五個質數; 不到一億的最大質數是一億減十一。
當管家一段時間後,我漸漸瞭解,博士不知道該說些什麼時。就會拿出數字來代替言語,他用這獨特的方法和別人交流。數字既相當於和對方握手時的右手,同時也是保護自己的大衣。這件厚重的大衣讓人無法觸及他的身體,也沒有一個人能夠脫下這件大衣。只要穿上這件大衣,他至少能夠保留自己的空間。(p11)
數字是博士的最愛,是博士與人溝通的工具,也是博士保護自己的大衣。
森林中的湖、沙漠中的綠洲
這裡有一種我不曾體驗過的靜謐,但並不是那種敲然無聲的寧靜,而是博士在數字森林徬徨時,充滿他內心的沈默,完全不受到掉落的白髮和霉菌的影響,將他重重包圍。就像隱藏在森林深處的湖一樣,是一種透明的沈默。(p20)
很有畫面的一段話,博士悠然自得的生活在數字森林當中,雖然只有80分鐘的記憶,又有誰,會認為他不快樂呢?
「對。無論再怎麼走,也看不到質數。放眼望去,四周都是沙漠。太陽無情照射,喉嚨乾渴,睜不開眼,眼前一片朦朧。以為『啊,是質數』,走近一看,卻是海市蜃樓。伸出雙手,只抓到一片熱風,仍然不肯輕易放棄,一步一步向前走。直到在地平線的那一端,找到有著一大片清澈的水,名為質數的綠洲。」(p81)
【數學世界】
質數 1到100的質數有25個,101200的質數有21個,201300的質數有16個,數字越大,就越難找到質數。因此,博士稱質數為沙漠中的綠洲。如何檢驗質數呢?
檢查一個正整數N是否為質數,最簡單的方法就是試除法,將該數N用小於等於√N的所有質數去試除,若均無法整除,則N為質數。例如100是否為質數,則用小於等於√100的的質數去試除(2, 3, 5, 7)。
博士與管家的友誼:友誼數
「你的生日是二月二十日。220,真是個聰明的數字。你看看這個,這是我在大學時代,憑一篇超越數論的論文獲得學長獎時得到的獎品.......」
......
「這不重要。你有沒有看到上面刻的數字?」
手錶背面刻著「學長獎」NO.284。(p22-23)
220和284有什麼關係?把220和284除了自己本身以外的因素都寫出來。
220:1、2、4、5、10、11、20、22、44、55、110
284:1、2、4、71、142
220:1+2+4+5+10+11+20+22+44+55+110 = 284
284:1+2+4+71+142 = 220
220的因數之和是284,284的因數之和是220。這是一對友誼數,是很難得的組合喔。不管是費瑪還是笛卡兒,都只找到一組而已,世上天安排下結合的數字。你不覺的很美嗎?你的生日和刻在我腕錶上的數字竟然有如此奇妙的關連。」(p26)
你找到了你的友誼數了嗎?茫茫人海中,我們總是期待可以找到瞭解自己的人,也期待被對方瞭解,就像220遇見了284。
來唱一首《你儂我儂》
「你儂我儂,特忒情多。情多處,熱如火。滄海可枯,堅石可爛。此愛、此情永遠不變。把一塊泥,捻一個你,留下笑容,使我長憶。再用一塊,塑一個我。長陪君旁,永伴君側。將咱兩個,一起打破。再將你我,用水調和。重新和泥,重新再做。再捻一個你,再塑一個我。從今以後,我可以說。我泥中有你 你泥中有我」,也像咖啡遇見奶茶一樣!
【數學世界】
友誼數 又稱為相親數,指兩個正整數中,彼此的全部約數之和(本身除外)與另一方相等。
320年左右,古希臘畢達哥拉斯發現的220與284,是人類認識的第一對相親數.
1636年,費馬發現了另一對相親數:17296和18416。
1638年,笛卡兒也發現了一對相親數:9363584和9437056。
1750年,歐拉一口氣向公眾拋出了60對相親數:2620和2924,5020和5564,6232和6368,……。
1866年,年方16歲的義大利青年巴格尼尼發現1184與1210是僅僅比220與284稍為大一些的第二對相親數。(書中p32及電影中都有提到)
畢達哥拉斯曾說:「朋友是你靈魂的倩影,要像220與284一樣親密。」
根號的寬大
「你是根號。這是一個面對任何數字都不會有絲毫為難之色,以寬大的胸懷加以包容的符號」(p36)
「沒有關係,放心吧。根號這個符號很牢固,會保護所有的數字」(p184)
第一句話是博士初認識管家的小孩時,在知道他的本名之前就已經給他起的暱稱。根號內可以是正數,可以是負數,也可以是零,所以根號以寬大的胸懷加以包容所有的數字。
第二句話是管家單擔心,根號出遊發生危險。博士以根號很牢固,會保護所有的數字,來比喻根號的勇敢與堅強。一語雙關的呈現,數學中根號的性質,與真實根號的特質。
【數學世界】
根號 對於非負實數x來說,平方根,是指平方結果等於x的實數,其中非負的平方根稱為算術平方根,用符號x表示,讀作根號x(![]() )。在複數系中,引入虛數單位 i,並規定
)。在複數系中,引入虛數單位 i,並規定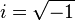 ,在此規定下,負數即可開平方。
,在此規定下,負數即可開平方。
完全數與江夏背號
博士撿起長椅下的樹枝,在地上寫了些什麼。除了「寫了些什麼」以外,我不知道還能用什麼來形容。有數字,有字母,也有神秘的符號......(略),枯枝將博士的意志刻在地上,不知不覺中,我們腳下變成了一片算式編織的雷絲圖案世界。
「我可不可以談一下我的發現?」
........
「把28所有的因數相加,還是等於28」
28 = 1+2+4+7+14
「是個完全數」(p56)
28正好是博士的偶像前阪神虎隊江夏豐的背號。這個寶貴的數字,體現了真正的完全,所有正因數的加總,恰恰好等於自己本身。如果從友誼數的觀點來看,完全數是一個很自戀的數字,自己喜歡自己。
【數學世界】
完全數 它所有的真因子(即除了自身以外的因數)的和,恰好等於它本身。最小的完全數是6,再來是28、496、8128。
6 = 1+2+3
28 = 1+2+4+7+14
496 = 1+2+4+8+16+31+62+124+248
8128= 1+2+4+8+16+32+64+127+254+508+1016+2032+4064
33550336(8位)
博士又拿起樹枝,雙腿縮進長椅下方,騰出一塊空地。
「完全數能以連續正整數和來表示。」(p58)
每個偶完全數都可以寫成連續自然數之和
6 = 1+2+3
28 = 1+2+4+5+6+7
496 = 1+2+3+4+5+6+7+8+.......+31
其他完全數共有的奇妙性質。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
發現上帝的筆記本
「當然,除了完全數之外,因數的和不是大於數字本身,就是小於數字本身。大於的時候,叫做盈數;小於的時候就叫做虧數。你不覺得這種命名方式很傳神嗎?18的因數和是 1+2+3+6+9 = 21,所以就是盈數。14的因數和是 1+2+7 = 10,所以就是虧數。」
我的腦海中浮現出14和18。聽了博士的說明後,才發現它們並非普通的數字。18在不為人知的情況下背負過剩的包袱;14則要默默面對殘缺的空白。
「因數和比數字本身小1的虧數不計其數,但比數字本身大1的盈數卻一個都不存在。不,或者應該說,至今還沒被人發現。」
「為什麼還沒發現?」
「因為,答案只寫在上帝的筆記本上。」(p58)
博士始終保持謙卑的心,努力的去發現上帝寫好的筆記本,發現數字間的的關係。他強調是發現,不是發明。數字的關係或數學的定理,早已存在某個不為人知的地方,就好像一字一句抄下記錄在上帝筆記本的真理一樣。誰都無法預知這本筆記本到底在哪裡,什麼時候打開。
【數學世界】
盈數 若一個正整數除了本身外之所有正因數之和比此數自身大。
虧數 若一個正整數除了本身外之所有正因數之和比此數自身小。
數學怎麼教?
從前讀書時,我只要看到數學課本就渾身發毛,如今卻能坦承接受博士教的數學問題。我並不是以管家的身份配合雇主的興趣,而是因為他懂得怎麼教。他看到算式時所發出的驚嘆、對美的稱讚,以及閃閃發亮的眼神,都令人感到意味深長。
最重要的是,因為他根本不記得曾經教過我,所以我可以毫無顧忌反覆問相同的問題。一般學生只要聽一遍就能理解,我卻需要五遍、十遍,才好不容易搞懂是怎麼回事。(p30)
這段對話點出了數學如何學的有趣?首先,老師必須熱愛所教的內容,就像博士談起數學就會「發出的驚嘆、對美的稱讚,以及閃閃發亮的眼神」,這是一個很高的境界。再者,就教學的態度而言,因為博士只有80分鐘的記憶,很有耐性的對待學生,不厭其煩的反覆教導,學生自然不會輕易的放棄。第三,就教學的方法而言,博士採用輔導的角色,不是直接告訴「管家或根號」答案,而是引導學生自己去思考,自己尋找答案。
台灣的教育過度的重視考試,受教育的目的似乎只為了「升學」,結果導致的是尋找「標準答案」。大大小小的考試,在講求「公平性」的考量下,大量的採用選擇題。在功利主義的導引下,學習經常失去了本身的純粹性與趣味性,因為反覆的練習追求熟練,但這絕對是失去樂趣得元凶。
一開始覺得很煩,後來卻產生了一種不甘心,甚至產生一種使命感。只有少數人知道這個算式背後的意義,很少人不曾感受過算式的意義就終老一生。(p68)
在博士的導引下,管家產生了以下三種層次的心境轉折:「很煩 → 不甘心→ 使命感」。這不就是教學的最高境界嗎?所謂的教學,就是「教」人怎麼「學」,從親身參與產生不甘心,再從樂趣產生了使命感。這是我努力的目標。
問題解法千百種
1+2+3+4+5+6+7+8+9+10 = ?
解法一:土法煉鋼
1+2+3+4+5+6+7+8+9+10 = 55
博士希望「根號」想一想還有沒有其他方法?
解法二:平均數法 (請參閱p70,根號從排隊發現的方法)
5為1到9的中位數,也為1到9的平均數。因此,
(1+2+4+5+6+7+8+9)+10 = (9×5)+10 =55(9個5再加10)→ 1/2[n×(n-1)]/n
解法三:三角形數(請參閱p87或 維基百科)
S = 1+2+3+4+5+6+7+8+9+10.......1
S = 10+9+8+7+6+5+4+3+2+1.......2
1+2
2×S = 11+11+11+11+11+11+11+11+11+11
S = (11×10)/2 = 55 → 1/2[n×(n+1)]
解法四:等差級數和(延伸)
博士讓管家及根號思考多種的解法,從代數的解法,到幾何的解法。其實數學的美,在於尋找上帝筆記本的邏輯思考過程,所以博士寄出了解題的投稿之後,並不在乎是不是第一個發現,也不在乎得到多少的獎金,因為在解題的過程,博士已經得到了滿足。
【數學世界】
三角形數 一定數目的點或圓在等距離的排列下可以形成一個等邊三角形(等差數列)
全壘打記錄到傳接球
「714次是貝布‧魯斯在1935年創下的全壘打記錄。1974年4月8日漢克·阿倫從道奇隊的阿爾‧道寧手中擊出的715隻全壘打,打破了這個記錄」
「714和715的積等於最小七個質數的積
714 × 715 = 2 × 3 × 5 × 7 × 11 × 13 × 17 = 510510」
「還有,714的質因數的和,與715質因數的和相等。
714 = 2 × 3 × 7 × 17
715 = 5 × 11 × 13
2 + 3 + 7 + 17 = 5 + 11 + 13
714是貝布‧魯斯一生打出的全壘打數,715是漢克·阿倫超越貝布‧魯斯的全壘打記錄。博士的座位號碼是「7-14」,根號的座位號碼是「7-15」,充滿著傳承的意味。而電影中導演,在電影的最後,以練傳接球來傳達這優美的意境。
《活著,就是創造自己的故事》是一本小川與河合的對話
小川:師徒兩人無比幸福地傳接球,就和前面提到的修繕和被修繕之間的關係一樣,指投對方接得到的球。
河合:所以,傳接球是很精彩的一幕,而且,球是最完美的事物。
小川:喔,對啊對啊,因為是零。
河合:一方面是零,另一方面是因為球體很完美。(p20)
傳接球是棒球比賽前熱身的練習,傳球者投出的球是要讓對方可以接的到,球是溝通的橋樑,就像小說中的數字,也像日常生活中我們使用的語言。我們會努力的使用對方可以理解的語言,對方感興趣的話題,傳達二個靈魂的心神交流。
【數學世界】
魯斯-阿倫數對 714 , 715
這個名字是因為漢克·阿倫在1974年4月8日9時7分以715次全壘打打破貝布·魯斯(Babe Ruth)的714次記錄,引起了魯斯-阿倫數對的發現者——Carol Nelson、David E. Penney和Carl Pomerance三人的靈感,從而發現714和715的特殊性質。
數學的目的 找出真理
正因為對實際生活沒有幫助,數字的秩序才顯得優美。(p147)
「瞭解了質數的性質,既不會給生活帶來方便,也賺不了錢。雖然數學本身遠離塵囂,仍然有許多數學的發現應用在現實生活中。橢圓的研究成為行星的軌道,愛因斯坦運用非歐基里得幾何學提出了宇宙的形狀。就連質數也成為密碼的基本,成為戰爭得幫凶,實在太醜陋了。但這些都不是數學的目的,數學只有一個目的,就是找出真理。」(p148)
相信大家都問過自己這個問題,學數學有什麼「用」,尤其是當我們數學考不及格的時候。就博士而言,學數學的唯一目的就是找出「真理」。所謂「知識求真、做人求善、藝術求美」,追求知識的過程即是在求真理。在唸書的時候,指導教授也跟我說過類似的話「瞭解問題的本質與解決問題同等的重要」。
杜威:「教育無外在目的,教育本身即是目的」,個人十分認同這個觀點。重視「過程」和「學習」的生活價值觀,過程本身就是一種目的和價值所在;學習本身是一種過程,學習本身即是價值所在。
「大學畢業即失業」,這句話背後隱藏的價值認為「大學應該是職業訓練所」? 大學,應該是通才教育,培養學生獨立思考的能力與解決問題的能力。而台灣過去20多年的廣設大學的政策下,高等教育的目的,從過去的培養社會菁英,到現在的普及平民教育。問題不在平民教育不好,而是社會結構體失衡,士不士、農不農、工不工、商不商,導致眼高手低的心態,不願從事基礎工作。
回歸原點的永恆
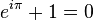
其中 e 是自然指數的底,i 是虛數單位,π 是圓周率。
e 的 π 和 i 之積的次方再加上 1 ,就變成了 0。(p163)
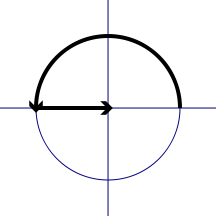
我重新看著博士的紙條。永無止盡地循環下去的數字,和讓人難以捉摸的虛數劃出簡潔的軌跡,在某一點落地。雖然沒有圓的出現,但來自宇宙的兀 飄 然來到 e 的身邊,和害羞的 i 握 着手。他們的身體緊緊的 靠 在一起,屏住呼吸,但有人加了1以後,世界就毫無預警的發生了巨大的變化,一切都歸於0。 (p163)
這個恆等式是「數學最奇妙的公式」,這一段話則是「本書最美的詩篇」。先從數學來看,歐拉恆等式把5個最基本的數學常數簡潔地連繫起來:
1 e 是自然指數的底(e = 2.71828......)是無理數
2 π 是圓周率(π =3.14159.......)也是無理數,半徑為1的半個圓周長
3 i 是虛數單位(i=![]() )
)
4 0 是加法的起點
5 1 是乘法的起點
數學的基本運算有三個:加法、乘法、次方。歐拉恆等式中,將原本不相干的五個常數,藉由三個運算,結合成一個優美的公式。小川用「飄」來表達數學的「次方」,用「握」、「靠」表達數學的「乘法」,加了1之後,一切歸於0。
再從圖形來詮釋歐拉恆等式,出發點是 1,經過了圓弧的半個周長 π ,來到了 -1,再加上 1之後,就回歸到 0。
在數學的二元的計算當中,1 代表 有,0 代表 無。
從人生來看,1 代表出生,0 代表死亡。每一個人從出生到死亡都走一段不一樣的里程,最後都終將回歸原點,回到永恆。
歐拉公式就像是暗夜中閃亮的一道流星,也像是刻在漆黑的洞窟裡的一行詩句。(p163)
走下圖書館的樓梯時,我回頭看了一下,數學書籍區仍然沒有一個人影, 一片寂靜,沒有人知道那裡隱藏著多麼美的事物。 (p164)
賢哥熱愛的算式
P0 =D0×(1+g)/(r-g)
g:盈餘(股利)成長率
r :需求報酬率
D0:今年的股利
P0:股票價值
這是一個股票投資很重要的公式,雖然經過了簡化,但卻是衡量股價昂貴或便宜的最重要公式。
到底要用多少價格買進一檔股票?依以下的步驟即可輕鬆得知:
1 找出企業股利的成長率 (g)
2 衡量個人的需求報酬率 (r)
3 代入今年的股利(D0)
即可找到合理的股價(P0)。本文不做公式由來的進一步推導,將留待《股票投資的五門課 企管篇》再詳細的說明。
買進一家公司的股票,成為了該公司的股東,預期未來股價會上漲及收到的現金股利。股價的波動是投資人無法預測的,但投資人可以預期的是每年收到的所有現金流量,並將個人要求的投資報酬率(r),將它折現成目前的價值。
希望沒有嚇到您,分享一個好用的Excel,簡單幫你算出未來八年預期的年化報酬率與股價的關係。其他的內容,就留待下回再分曉。
由於本篇閱讀心得的關係,時間被小說與數學綁架了。
耽誤了《股票投資的五門課 企管篇》,只好請各位再等一等。未來,部落格的文章將走向精緻化。
